Lanthanide Ion 4f Electron Densities
Published:
If you want to plot or visualise 4f charge densities, then look no further.
Sievers Approach
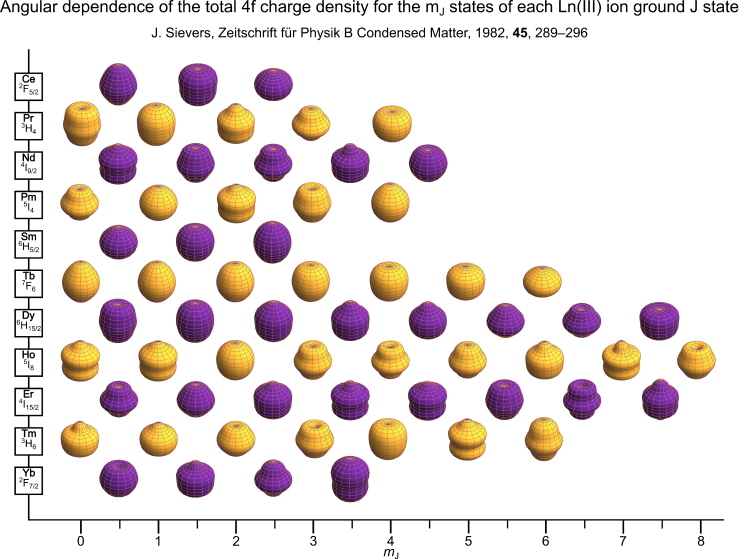
These are the free-ion charge density plots for the $m_J$ states of the ground Hund’s rule term of each Ln(III) ion as calculated and derived by Sievers . The plot is produced in the same style as Reinhart and Long but instead uses The University of Manchester’s gold and purple colours. Eu(III) and Gd(III) are missing as they have $J=0$ and $L=0$ ground states respectively.
A high-resolution version of this plot is available here.
Each spheroid is calculated using a radius vector $R(\phi)$ which is a function of the polar angle $\phi$. This vector describes the angular dependence of the electron or charge density of a given $m_J$ state.
\[R(\phi) = \sqrt[3]{\tilde{c}_0 + \sum_{i=2,4,6}c_i Y_{i,0}(\phi)}\]where $ \tilde{c}_0 = 3\pi/4 $ .
The $Y_{k0}$ are spherical harmonics, while the values $ c_k $ are listed by Sievers for the Ln(III) ions in terms of $A_k$, and can be calculated for other oxidation states using the procedure he outlines.
The conversion from $A_k$ to $c_k$ is straightforward
\[A_k = \sqrt{4\pi/(2k+1)}c_k\]The $A_k$ values given by Sievers can be downloaded as a text file here.
